Activity 5: Physical Measurements from DFT

In this activity we are asked to create a frequency scale for Fourier Transform analysis. For a 2 dimensional system, the Discrete Fourier Transform can be represented as,

Using the given code below to display the fftshifted output of a temporal sound, some parameters were varied to answer the given questions.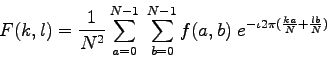

T = 2;
N = 256;
dt = T/256;
t = [0:dt:(N-1)*dt];
f = 5;
y = sin(2*%pi*f*t);
f1 = scf(1); plot(t,y);

FY = fft(y);
F = 1/(2*dt);
df = 2*F/256;
f = [-(df*(N/2)):df:df*(N/2 -1)];
f2 = scf(2); plot(f, fftshift(abs(FY)));

The generated 1D sinusoid in the form of sin(2*pi*f*t) is shown below along with its fftshifted output. The output of the DFT transformation represents the image in the Fourier/frequency domain, whereas the input image is the equivalent spatial domain. In the Fourier domain image, each point represents a particular frequency contained in the spatial domain image.
When DFT is applied on images, the image would contain the components of all frequencies, but their magnitude gets smaller for higher frequencies. Therefore, low frequencies contain more image information than the higher ones. The transformed image also shows the two dominating directions in the Fourier image, one passing vertically and one horizontally through the center, originating from the regular patterns in the background of the original image.

For the following questions:

a) Light from a fluorescent lamp is known to flicker at 120Hz. What should be the threshold sampling interval for accurate FT analysis?

-- The Nyquist theorem states that the maximum frequency that can be accurately represented is less than half of the sampling rate. For a fluorescent lamp that flickers at 120Hz, it should be sampled at least twice that fast at about 24oHz, and therefore must have a threshold sampling interval of t=1/240Hz.

b) What is the effect of increasing the number of samples N in the FT?



-- Increasing the number of samples N would make the fourier transform of an input more accurate since more points from the waveform of the input are regenerated in the waveform of the output. From the plot on the left, it can be seen that the frequency domain increases.





c) What is the effect of decreasing the sampling interval Δt in the FT?

-- From the Nyquist Theorem, if the sampling interval is decreased, the maximum frequency that can be detected without any distortion of the input will be increased. Therefore, if the sampling interval is below the threshold frequency, there will be an inaccurate reconstruction of the input due to aliasing.

d) What is the effect of fixing the total time interval T but increasing the
number of samples N?

-- Increasing the samples while fixing T will not have much effect on the frequency domain. It will only decrease dt and half the amplitude by N because of the increased number of samples.

rating-9, because although I think I am fine with the theoretical, few simulations were done.

Acknowledgement:
Paul -for giving me some important notes.