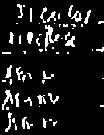Activity 11: Camera Calibration

In this activity, we were asked to transform a global coordinate system to an image-plane centric coordinate system through translation and rotation processes to calibrate a camera.

Camera calibration involves the calculation of parameters aij of a matrix A. This matrix determines the camera geometry. Below are the equations used for this activity.

To start with the activity, a picture of a checkerboard image shown below was taken. The origin was chosen to be at the lower middle part of the image, thus letting the left side be the x axis, the right side as the y axis, and the z axis as the vertical. 25 corners of the squares of the image were chosen to be measured.

Using the locate function in Scilab, the coordinates of the chosen points were determined.
These values were tabulated below with their corresponding calculated 2D coordinate values using the code. Results show that there is an ave. %difference of 1.48 and 1.82 for the y and z values respectively.

yi	zi	Calculated yi	Calculated zi
57.95	232.7	57.02	239.29
97.74	236.8	97.05	237.22
182.26	234.46	181.02	232.41
249.71	228.01	252.74	226.59
93.72	189.88	94.94	192
161.17	196.92	162.46	193.44
213.34	186.95	212.5	186.76
284.31	178.15	289.25	176.5
53.95	142.96	53.33	144.06
73.15	149.41	73.76	145.88
164.66	151.76	160.04	153.54
227.42	140.62	227.5	141.3
51.53	98.39	51.24	97.49
127.16	110.7	126.03	109.15
177.57	108.36	173.43	110.48
243.26	92.52	242.91	94.58
67.3	59.09	69.45	56.04
125.98	69.06	123.73	68.09
161.14	71.41	155.3	75.09
223.31	54.4	221.55	56.81
83.72	17.55	86.4	17.46
137.23	33.28	137.63	32.14
174.63	31.59	168.47	31.53
222.73	15.93	218.62	15.34

The code used for this is:

chdir('F:\186\activity11');
im = imread('image3.jpg');
image = im2gray(im);
imshow(image);
x = locate(25,1);
yi = x(1,:);
zi = x(2,:);

xo = [6 4 0 0 4 0 0 0 6 5 0 0 6 2 0 0 5 2 0 0 4 1 0 0 0];
yo = [0 0 1 5 0 0 3 7 0 0 0 4 0 0 1 5 0 0 0 4 0 0 1 4 6];
zo = [10 10 10 10 8 8 8 8 6 6 6 6 4 4 4 4 2 2 2 2 0 0 0 0 0];

for i=1:length(xo)
Q1 = [xo(i) yo(i) zo(i) 1 0 0 0 0 -(yi(i)*xo(i)) -(yi(i)*yo(i)) -(yi(i)*zo(i))];
Q2 = [0 0 0 0 xo(i) yo(i) zo(i) 1 -(zi(i)*xo(i)) -(zi(i)*yo(i)) -(zi(i)*zo(i))];
d1 = yi(i);
d2 = zi(i);
end
a = inv(Q'*Q)*Q'*d;
for j = 1:length(xo)
y2 = ((a(1)*xo(j))+(a(2)*yo(j))+(a(3)*zo(j))+a(4))/((a(9)*xo(j))+(a(10)*yo(j))+(a(11)*zo(j))+1);
z2= ((a(5)*xo(j))+(a(6)*yo(j))+(a(7)*zo(j))+a(8))/((a(9)*xo(j))+(a(10)*yo(j))+(a(11)*zo(j))+1);
end

rating-9 because the ave. percentage difference between the located and calculated coordinate values is still within allowable 5% .

acknowledgement - Lei for helping me with some of the processes involved.

Activity10: Preprocessing Handwritten Text

In this activity, we were asked to use different image processing techniques to extract handwritten texts from an imaged document with lines.

To start with the activity, the following image was downloaded and a portion of it was cropped. This image will be processed such that the horizontal lines will be removed from the image and only the handwritten text will remain.

After applying fftshift to the image the resulting FT image is,

Then, after processing the image, the resulting image shows that the horizontal lines were removed as shown below.



The image was then binarized to clean the image of any unneeded pixels. The binarized image was also applied with opening operation using a 2x2 structuring element and the resulting image is shown below. Compared with the original image shown at the left, most of the horizontal lines were removed but the image texts were not reconstructed clear enough.



The code used for this activity is:

chdir('G:\186\activity10');
cropim = gray_imread('cropim2.jpg');
a1 = fftshift(fft2(cropim));
imshow(abs(a1), []);

[x,y]=size(a1);
a2=a1(:,:);
filter=ones(i,j);
for n=j/2-2:j/2+2
for m=1:i/2-2
filter(m,n)=0;
end
for m=i/2+ 2 : i
filter(m,n)=0;
end
end
a2=filter.*a1;
imshow(abs(a2), []);

fftim=abs(fft2(a2));
imshow(fftim, []);

grayim = gray_imread('fftim.bmp');
grayim = 1-grayim;
imbin = im2bw(grayim,0.5);
imshow(imbin);

square = ones(2,2);
im=erode(imbin,square );
im=dilate(im,square );
im=erode(im,square );
im=dilate(im,square );
imfinal=im;
imshow(imfinal);
[L,n] = bwlabel(imfinal);

rating-8, because the resulting image is not clear.
Acknowledgements: Jeric and Angel for helping me with the removal of horizontal lines.

Activity 9: Binary Operations

In this activity, application of what we have learned so far were applied to determine the best estimate of the area (in pixel count) of simulated cells. These cells are represented as images of scattered holes as shown below.




To start with the activity, the first image was used and was subdivided into 256x256 images. For each grayscaled subimage, its histogram was plotted to determine its threshold value, thus allowing the cell to be separated from its background. Then, the images were binarized using 'im2bw' from Scilab.

Morphological operations such as dilation and erosion were then applied to perform the opening and closing operations to the images. In opening, erosion followed by dilation were applied to an image. Whereas in closing, dilation followed by erosion were applied to the image. The opening and closing operations were done to clean images of isolated pixels or small holes in the cells that may interrupt with the estimation of the cell area.

A subimage is shown here with its: binarized form, with the application of closing operation, then by opening operation, and lastly, with the application of bwlabel to label each blob with different colors.



Using 'for loop', the estimated area for each blob of all the subimages were determined. The histogram showing the area vs. frequency is shown below.


From the histogram, it can be seen that the calculated blob area with the highest frequency is below 1000. This histogram however cannot clearly show what exactly is the most frequent area.

By tallying all the areas for each subimage, the estimated area of each blob was found to have a value of '489.75 pixels' and a standard deviation of '31.5' which agrees with the plotted histogram above.

The program used for this activity is:

chdir('F:\186\activity9');
agray = gray_imread('c1-1.jpg');
abin = im2bw(agray, 211/256);
imshow(abin);
se1=ones(4,4);

squareimg = imread('bin-c1-2.bmp');
img=img(:,:,1);
scf(1);
subplot(2,2,1);
imshow(img);

dil1=dilate(img,se1);
er1=erode(dil1, se1); //closing
subplot(2,2,2);
imshow(er1);
cl1=erode(img, se1); //opening
di1=dilate(cl1, se1);
subplot(2,2,3);
imshow(cl1);

[L,n] = bwlabel(cl1);
for j = 1:n //area
r= (L==j);
A(c) = sum(r);
c = c + 1;endend
histplot(length(A),A);

x= find(A>450 & A<600);>

a = sum(A(x))/length(x)

stdev = stdev(A(x))

----------------------------

rating- 8, because the estimated area has a 7.5% difference with respect to the theoretical value which is 530.

Acknowledgements: Marge, paul and angel for helping me with the opening and closing concepts of the activity.

Activity 8: Morphological Operations

In this activity, we are asked to perform different Morphological Operations such as Dilation and Erosion to modify images.

Given a binary image A and a structuring image B, the dilation of A by B results to an elongated or expanded image of A. Here, for each pixel in A superimpose the origin of B, as long as the origin is within A, its pixel value is retained. Otherwise the pixel value is deleted resulting to the erosion of A by B, and thus, a reduced image of A.

The binary images used in this activity are shown below:

square(50x50 ), triangle(base=50, height=30), circle(radius=25), hollow square(60x60, with 4pixel thick edges), cross(8pixels thick, 50pixels long)

The following figures are the given binary images applied with Dilation and then by Erosion Operation. For each operation, the binary images were dilated/eroded with the given structuring elements : 4x4 ones, 2x4 ones, 4x2 ones, and a cross (5pixels long, 1 pixel thick) respectively.

Square: Dilation and Erosion

Triangle: Dilation and Erosion

Circle: Dilation and Erosion

Hollow square: Dilation and Erosion

Cross: Dilation and Erosion


rating - 9, because although I got the correct output images in my simulations, some of the predicted images I drew were wrong.

Acknowledgements: Lei and marge - for helping me with the prediction of the output images

Activity 7: Enhancement in the Frequency Domain

In this activity which is divided into three parts, we are generally asked to apply Fourier transform for the enhancement of frequency domains.

Part A. Anamorphic Property of the Fourier Transform

For the first activity, we were first asked asked to create 2D sinusoids in the X direction. The images below are the sinusoids for frequencies of 4, 12 and 20 respectively.



The fourier transforms for the respective sinusoids above are shown below. It can be observed that the greater the frequency value, the farther the white dots are from the center. This is expected. Therefore, it was shown that the frequency of a sinusoid varies proportionally with the distance of the white dot from the image center.



For a constant frequency of 4, the sinusoids were rotated at different theta: 30, 60 and 90 degrees respectively with respect to the vertical axis. The images are shown below.



The resulting FT images show that the dots were also rotated by the same angle. Since the images were in the inverse space, they are directed in the opposite direction. This is as expected of 2D FT images, where rotation of the sinusoids results to the rotation of their FT.



The product of the combination of the 2 sinusoids running in the X and Y directions is shown below with its corresponding FT. The resulting product is like a checkerboard with its alternating white and black square parts, whereas its FT image consists of 4 white dots. Since the dots are located such that it forms like a square, the inversion of the X and Y axes for this FT image is not that evident.



nx = 100; ny = 100;
x = linspace(-1,1,nx);
y = linspace(-1,1,ny);
[X,Y] = ndgrid(x,y);
f = 4 //frequency
z = sin(2*%pi*f*X);nx = 100; ny = 100;
FTz = abs(fft(z));
FFTz = abs(fftshift(FTz));
//imshow(FFTz,[]);

theta = 30;
rotated = sin(2*%pi*f*(Y*sin(theta) + X*cos(theta)));
imshow(rotated,[]);
FTrotated = abs(fft(rotated));
FFTrotated = abs(fftshift(FTrotated));
imshow(FFTrotated,[]);

product = sin(2*%pi*4*X).*sin(2*%pi*4*Y);
//imshow(product,[]);
FTproduct = abs(fft(product));
FFTproduct = abs(fftshift(FTproduct));
imshow(FFTproduct,[]);

Part B. Fingerprints: Ridge Enhancement

For this part of the activity, we were asked to obtain an FT image of a grayscaled fingerprint image, and to determine where the frequencies of the fingerprint ridges are located. This is to enhance the original image by filtering.

The figures below are: the original image, the mean-centered image, its FT image,the filter and the enhanced images.





Here, a high pass filter, was used here to increase the components of the high-frequency and separate it from low-frequency components. This would therefore result in the enhancement of the fingerprint ridges.

It can be observed that fingerprint ridges was enhanced in the output image using the high-pass filter. But, the result was not that clear for the upper and lower parts of the image. The filter radius was varied many times, but the resulting images has more or less the same blurr as the one presented above. Therefore, I think that my program works best for the enhancement of images with lesser blotches or defects than my original image.

fprint = gray_imread('fingerprint.bmp');
fprintmean = fprint-mean(fprint);
imshow(fprintmean);
FT2fprint1 = fft2(fprintmean);
product = real((FT2fprint1).*conj(FT2fprint1));
imshow(fftshift(log(product+1)),[]);
filter = mkfftfilter(fprintmean,'exp',5);
imshow(filter);
FT2fprint2 = FT2fprint1.*fftshift(1-filter);
Image = real(fft2(FT2fprint2));
imshow(Image);

Part C: Lunar Landing Scanned Pictures: Line Removal

For this part, filtering in the Frequency domain was to be done to remove the vertical lines from the given image below. This was first done by applying fft to the grayscaled image of the lunar landing. Using a filter formed through mkfftfilter() of Scilab, it can be observed that white lines were produced by the frequency components. Using a band pass filter between 20 and 100, the last image was formed. Although the resulting image is quite blurry, the aim of the activity which is to remove the vertical lines in the image was accomplished. When the range of the bandpass filter was varied, the vertical lines appeared. Therefore, this is the best image I got so far.



a = imread('moon.bmp');
moon = im2gray(a);
moonmean = moon-mean(moon);
imshow(moonmean);

FTmoon = fft2(moonmean);
product = real((FTmoon).*conj(FTmoon));
imshow(fftshift(log(product+1)),[]);

filter1 = mkfftfilter(moonmean,'binary',100);
filter2 = mkfftfilter(moonmean,'binary',20);
f = filter1-filter2;
image = FTmoon.*fftshift(1-f);
image2 = real(fft2(image));
imshow(image2,[]);

rating - 9 because although I think I did fine in this activity, I was not able to simulate much better output images than those figures I have presented.

Acknowledgement: Angel - for helping me with the enhancement of the fingerprint.