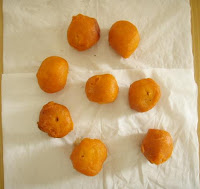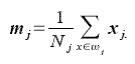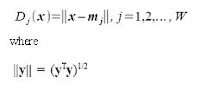In this activity, we were asked to perform classification of different images through pattern recognition. This would be done by assembling different objects, which can be classified into 2 to 5 classes. Half of these will serve as training sets, whereas the other half will serve as test sets. These training set are used to distinguish one class from another.
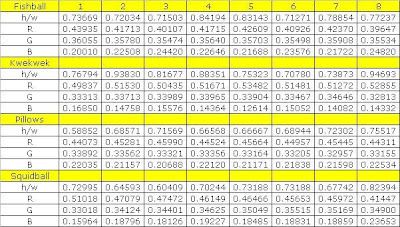
The objects used were fishballs, kwekwek, pillows, and squidballs. I assembled 8 pieces of each of the objects, and classified them using 4 features , which are, the ratio between the height and the width, and each of their R-G-B values.
The objects used are shown below.

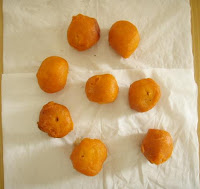


The images were first converted into grayscale before the threshold value of the images were determined using their histogram, to be able to properly binarized it.
The feature vectors are represented by x, and N is the number of the objects in the each class j.
Below are the feature vectors of the objects.
To determine in which class an unknown feature vector belongs, the feature vector mean given by the equation below is taken.
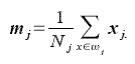
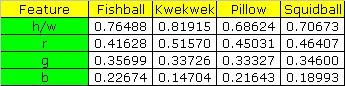
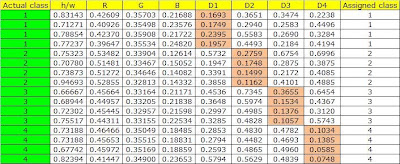
The calculated means are tabulated below.
The calculated mean will then be used to determine the Euclidean distance, D.
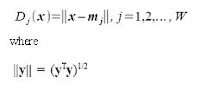
Finally, the class in which minimum Euclidean distance was calculated, is the assigned class of x.
Results from the table below show that 100% of the objects were properly classified.
rating: 10 because proper classification of the objects was done!
acknowledgement: Angel and Marge for helping me with the program.